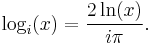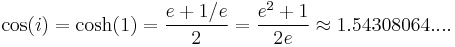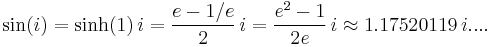Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial P(x) (see algebraic closure and fundamental theorem of algebra). The imaginary unit is most commonly denoted by i, but in contexts where i is ambiguous or problematic j, or the Greek ι (see alternative notations), is sometimes used. The imaginary unit's core property is that i2 = −1. The term "imaginary" is used because there is no real number having a negative square.
There are in fact two square roots of −1, namely i and −i, just as there are two square roots of every other real number, except zero, which has one double square root.
In the disciplines of electrical engineering and control systems engineering, the imaginary unit is often denoted by j instead of i, because i is commonly used to denote electric current in these disciplines.
For a history of the imaginary unit, see Complex number: History.
Contents |
Definition
 (repeats the pattern from blue area) (repeats the pattern from blue area) |
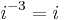 |
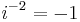 |
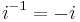 |
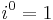 |
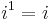 |
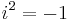 |
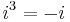 |
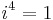 |
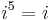 |
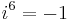 |
 (repeats the pattern from blue area) (repeats the pattern from blue area) |
An imaginary number is a real number multiplied by the imaginary unit i, which is defined by its property i2 = −1.[1] The square of an imaginary number is less than or equal to zero. For example, 5i is an imaginary number and its square is −25. According to some definitions, zero (0i) is not regarded as an imaginary number, but as a pure real.
An imaginary number bi can be added to a real number a to form a complex number of the form a + bi, where a and b are called, respectively, the real part and the imaginary part of the complex number. Imaginary numbers can therefore be thought of as complex numbers whose real part is zero. The name "imaginary number" was coined in the 17th century as a derogatory term, as such numbers were regarded by some as fictitious or useless, but today they have a variety of essential, concrete applications in science and engineering.
Although the construction is called "imaginary", and although the concept of an imaginary number may be intuitively more difficult to grasp than that of a real number, the construction is perfectly valid from a mathematical standpoint. Real number operations can be extended to imaginary and complex numbers by treating i as an unknown quantity while manipulating an expression, and then using the definition to replace any occurrence of i 2 with −1. Higher integral powers of i can also be replaced with −i, 1, i, or −1:
Similarly,
i and −i
Being a quadratic polynomial with no multiple root, the defining equation x2 = −1 has two distinct solutions, which are equally valid and which happen to be additive and multiplicative inverses of each other. More precisely, once a solution i of the equation has been fixed, the value −i, which is distinct from i, is also a solution. Since the equation is the only definition of i, it appears that the definition is ambiguous (more precisely, not well-defined). However, no ambiguity results as long as one of the solutions is chosen and fixed as the "positive i". This is because, although −i and i are not quantitatively equivalent (they are negatives of each other), there is no algebraic difference between i and −i. Both imaginary numbers have equal claim to being the number whose square is −1. If all mathematical textbooks and published literature referring to imaginary or complex numbers were rewritten with −i replacing every occurrence of +i (and therefore every occurrence of −i replaced by −(−i) = +i), all facts and theorems would continue to be equivalently valid. The distinction between the two roots x of x2 + 1 = 0 with one of them as "positive" is purely a notational relic; neither root can be said to be more primary or fundamental than the other.
The issue can be a subtle one. The most precise explanation is to say that although the complex field, defined as R[x]/(x2 + 1), (see complex number) is unique up to isomorphism, it is not unique up to a unique isomorphism — there are exactly 2 field automorphisms of R[x]/(x2 + 1) which keep each real number fixed: the identity and the automorphism sending x to −x. See also Complex conjugate and Galois group.
A similar issue arises if the complex numbers are interpreted as 2 × 2 real matrices (see matrix representation of complex numbers), because then both
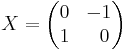 and
and 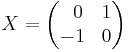
are solutions to the matrix equation
In this case, the ambiguity results from the geometric choice of which "direction" around the unit circle is "positive" rotation. A more precise explanation is to say that the automorphism group of the special orthogonal group SO (2, R) has exactly 2 elements — the identity and the automorphism which exchanges "CW" (clockwise) and "CCW" (counter-clockwise) rotations. See orthogonal group.
All these ambiguities can be solved by adopting a more rigorous definition of complex number, and explicitly choosing one of the solutions to the equation to be the imaginary unit. For example, the ordered pair (0, 1), in the usual construction of the complex numbers with two-dimensional vectors.
History
Although Greek mathematician and engineer Heron of Alexandria is noted as the first to have conceived these numbers,[2][3] Rafael Bombelli first set down the rules for multiplication in the complex numbers in 1572. The concept had appeared in print earlier, for instance in work by Gerolamo Cardano. At the time, such numbers were poorly understood and regarded by some as fictitious or useless, much as zero and the negative numbers once were. Many other mathematicians were slow to adopt the use of imaginary numbers, including René Descartes, who wrote about them in his La Géométrie, where the term imaginary was used and meant to be derogatory.[4] The use of imaginary numbers was not widely accepted until the work of Leonhard Euler (1707–1783) and Carl Friedrich Gauss (1777–1855). The geometric significance of complex numbers as points in a plane was first found by Caspar Wessel (1745–1818).[5]
In 1843 a mathematical physicist, William Rowan Hamilton, extended the idea of an axis of imaginary numbers in the plane to a three-dimensional space of quaternion imaginaries.
With the development of quotient rings of polynomial rings, the concept behind an imaginary number became more substantial, but then one also finds other imaginary numbers such as the j of tessarines which has a square of +1. This idea first surfaced with the articles by James Cockle beginning in 1848.
Proper use
The imaginary unit is sometimes written √−1 in advanced mathematics contexts (as well as in less advanced popular texts). However, great care needs to be taken when manipulating formulas involving radicals. The notation is reserved either for the principal square root function, which is only defined for real x ≥ 0, or for the principal branch of the complex square root function. Attempting to apply the calculation rules of the principal (real) square root function to manipulate the principal branch of the complex square root function will produce false results:
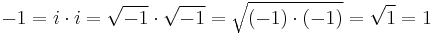 (incorrect).
(incorrect).
Attempting to correct the calculation by specifying both the positive and negative roots only produces ambiguous results:
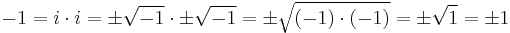 (ambiguous).
(ambiguous).
Similarly:
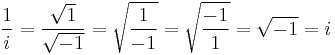 (incorrect).
(incorrect).
The calculation rules
and
are only valid for real, non-negative values of a and b.
These problems are avoided by writing and manipulating i√7, rather than expressions like √−7. For a more thorough discussion, see Square root and Branch point.
Geometric interpretation
Geometrically, imaginary numbers are found on the vertical axis of the complex number plane, allowing them to be presented perpendicular to the real axis. One way of viewing imaginary numbers is to consider a standard number line, positively increasing in magnitude to the right, and negatively increasing in magnitude to the left. At 0 on this  -axis, a
-axis, a  -axis can be drawn with "positive" direction going up; "positive" imaginary numbers then increase in magnitude upwards, and "negative" imaginary numbers increase in magnitude downwards. This vertical axis is often called the "imaginary axis" and is denoted
-axis can be drawn with "positive" direction going up; "positive" imaginary numbers then increase in magnitude upwards, and "negative" imaginary numbers increase in magnitude downwards. This vertical axis is often called the "imaginary axis" and is denoted 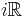 ,
, 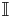 , or simply
, or simply 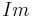 .
.
In this representation, multiplication by –1 corresponds to a rotation of 180 degrees about the origin. Multiplication by  corresponds to a 90-degree rotation in the "positive" direction (i.e., counterclockwise), and the equation
corresponds to a 90-degree rotation in the "positive" direction (i.e., counterclockwise), and the equation 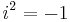 is interpreted as saying that if we apply two 90-degree rotations about the origin, the net result is a single 180-degree rotation. Note that a 90-degree rotation in the "negative" direction (i.e. clockwise) also satisfies this interpretation. This reflects the fact that
is interpreted as saying that if we apply two 90-degree rotations about the origin, the net result is a single 180-degree rotation. Note that a 90-degree rotation in the "negative" direction (i.e. clockwise) also satisfies this interpretation. This reflects the fact that 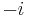 also solves the equation
also solves the equation 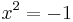 — see imaginary unit. In general, multiplying by a complex number is the same as rotating around the origin by the complex number's argument, followed by a scaling by its magnitude.
— see imaginary unit. In general, multiplying by a complex number is the same as rotating around the origin by the complex number's argument, followed by a scaling by its magnitude.
Properties
Square roots
The square root of i can be expressed as either of two complex numbers[nb 1]
Indeed, squaring the right-hand side gives
This result can also be derived with Euler's formula
by substituting x = π/2, giving
Taking the square root of both sides gives
which, through application of Euler's formula to x = π/4, gives
Similarly, the square root of -i can be expressed as either of two complex numbers using Euler's formula:
by substituting x = 3π/2, giving
Taking the square root of both sides gives
which, through application of Euler's formula to x = 3π/4, gives
Multiplying the square root of i by i also gives:
Multiplication and division
Multiplying a complex number by i gives:
Dividing by i is equivalent with multiplying by the reciprocal of i:
Using this identity to generalize division by i to all complex numbers gives:
Powers
The powers of i repeat in a cycle expressible with the following pattern, where n is any integer:
This leads to the conclusion that
where mod 4 represents arithmetic modulo 4.
i raised to the i power
Making use of Euler's formula, ii is
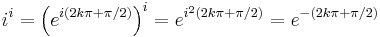 where
where 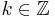 , the set of integers.
, the set of integers.
The principal value for (k = 0) is 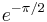 or approximately 0.207879576350761908546955465465465...[6]
or approximately 0.207879576350761908546955465465465...[6]
Factorial
The factorial of the imaginary unit i is most often given in terms of the gamma function evaluated at 1 + i:
Also,
Other operations
Many mathematical operations that can be carried out with real numbers can also be carried out with i, such as exponentiation, roots, logarithms, and trigonometric functions.
A number raised to the ni power is:
The nith root of a number is:
The imaginary-base logarithm of a number is:
As with any complex logarithm, the log base i is not uniquely defined.
The cosine of i is a real number:
And the sine of i is purely imaginary:
Applications of imaginary numbers
Imaginary numbers are useful because they allow the construction of non-real complex numbers, which have essential concrete applications in a variety of scientific and related areas such as signal processing, control theory, electromagnetism, fluid dynamics, quantum mechanics, cartography, and vibration analysis.
Alternative notations
- In electrical engineering and related fields, the imaginary unit is often denoted by j to avoid confusion with electrical current as a function of time, traditionally denoted by i(t) or just i. The Python programming language also uses j to denote the imaginary unit. MATLAB associates both i and j with the imaginary unit, although 1i is preferable, for speed and improved robustness.[8]
- Some sources define j = −i, in particular with regard to traveling waves (e.g., a right traveling plane wave in the x direction)
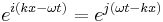 .
. - Some texts use the Greek letter iota (ι) for the imaginary unit, to avoid confusion, esp. with index and subscripts. See Biquaternion.
See also
Notes
- ^ To find such a number, one can solve the equations
- (x + iy)2 = i
- x2 + 2ixy − y2 = i
- x2 − y2 + 2ixy = 0 + i
- x2 − y2 = 0
- 2xy = 1
- x2 − 1/4x2 = 0
- x2 = 1/4x2
- 4x4 = 1
References
- ^ Uno Ingard, K. (1988), Fundamentals of waves & oscillations, Cambridge University Press, p. 38, ISBN 0-521-33957-X, http://books.google.com/books?id=SGVfGIewvxkC, Chapter 2, p 38
- ^ Hargittai, István (1992). Fivefold symmetry (2nd ed.). World Scientific. p. 153. ISBN 981020600-3. http://books.google.com/books?id=-Tt37ajV5ZgC., Extract of page 153
- ^ Roy, Stephen Campbell (2007). Complex numbers: lattice simulation and zeta function applications. Horwood. p. 1. ISBN 190427525-7. http://books.google.com/books?id=J-2BRbFa5IkC.
- ^ Martinez, Albert A. (2006), Negative Math: How Mathematical Rules Can Be Positively Bent, Princeton: Princeton University Press, ISBN 0691123098, discusses ambiguities of meaning in imaginary expressions in historical context.
- ^ Rozenfeld, Boris Abramovich (1988). A history of non-euclidean geometry: evolution of the concept of a geometric space. Springer. p. 382. ISBN 0-387-96458-4. http://books.google.com/books?id=DRLpAFZM7uwC., Chapter 10, page 382
- ^ "The Penguin Dictionary of Curious and Interesting Numbers" by David Wells, Page 26.
- ^ "abs(i!)", WolframAlpha.
- ^ "MATLAB Product Documentation". http://www.mathworks.com/help/techdoc/ref/i.html.
Further reading
- Nahin, Paul J. (1998). An Imaginary Tale: The Story of √−1. Chichester: Princeton University Press. ISBN 0691027951.
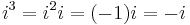
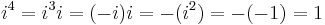
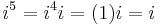
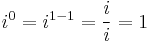
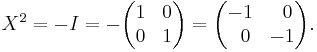
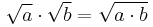
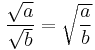
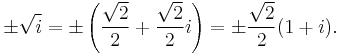
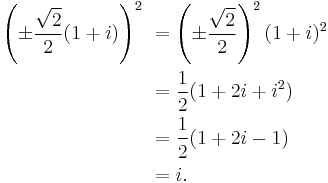
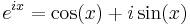
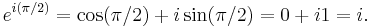
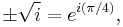
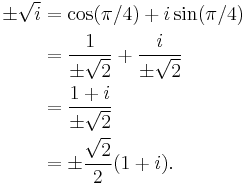
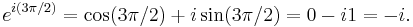
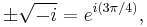
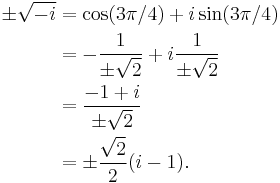
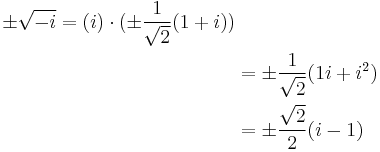
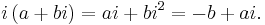
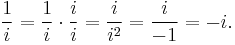
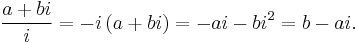
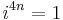
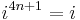
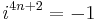
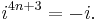
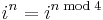
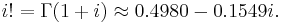
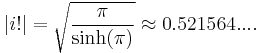
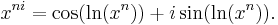
![\!\ \sqrt[ni]{x} = \cos(\ln(\sqrt[n]{x})) - i \sin(\ln(\sqrt[n]{x})).](/2012-wikipedia_en_all_nopic_01_2012/I/a0fbe6b07abd5861871b5f8af81f82a4.png)